Interval Inversions
From “Interval Inversions¨ in Music Theory for Electronic Music Producers
Just like a chord can be inverted, so can individual intervals. For exampl: the note C up to the note G is a fifth. But the notes G up to C is a fourth. That is because the intervals are inverted.
For more on chord inversions, especially for triads, see 20240928141202-Shape_of_Chord_Progressions. While chord inversions are related to the default “root position¨ of a triad, interval inversions are simply reversing the given notes that are the start and end of the interval within a certain key of a scale (see 20240903174948-Being_“In_Key” & 20240904142215-Figuring_out_the_Scale). Keep in mind that changing the start means changing from what (mechanical) key, or corresponding in-tune pitch, one is counting half-steps from. That is, it is not a reversal of the counting procedure on the same set of (mechanical) keys / pitches, but a reversal of the (mechanical) keys or pitches that form the initial state and desired terminus of the procedure.
Interval inversion as misnomer
In other words, the intervals in the triad itself are not necessarily what are inverted, despite the name; instead, the starting and ending notes of the triad are flipped, which then causes a potential change in the intervals comprising the triad.
In addition to that, given said interval is within a certain key of a scale from a standard Western classical piano keyboard , the interval can actually change when the initial and terminal state of the counting procedure are flipped. Hence, while “the note C up to the note G is a fifth. […] the notes G up to C is a fourth¨ (Allen 2018, 92). That is in fact how the half-steps of intervals are counted; see 20240901171406-Musical_Intervals & Chromatic Interval Variability of Diatonic Chords.
Intervals as Diatonic Counts and Half-Steps as Chromatic Moves
Consequently, the number that describes the interval is not the same as the quantity of half-steps in the interval. The former describes a count of diatonic (mechanical) keys or notes running from start to end while the latter describes a quantity of movements made to get from an initial chromatic (mechanical) key to the final one. See 20240927133630-What_is_a_Diatonic_Chord_Progression.
Perfect and “Imperfect¨ Inversions
Note that the quality of an interval of a fourth (refer to 20240901171406-Musical_Intervals), i.e. an inversion of a perfect fifth, is “perfect¨:
From “Interval Inversions¨ in Music Theory for Electronic Music Producers
The rule is that whenever you invert a chord, it changes to a new interval name with the opposite quality. The exception is the perfect fifth, which inverts to another perfect interval (perfect fourth).
The below is a perfect fourth interval; based on the musical alphabet on the standard Western classical piano, we know this goes from G to C (refer to 20240831190951-Musical_Alphabet & 20240901115917-Locating_C_Piano_Key):
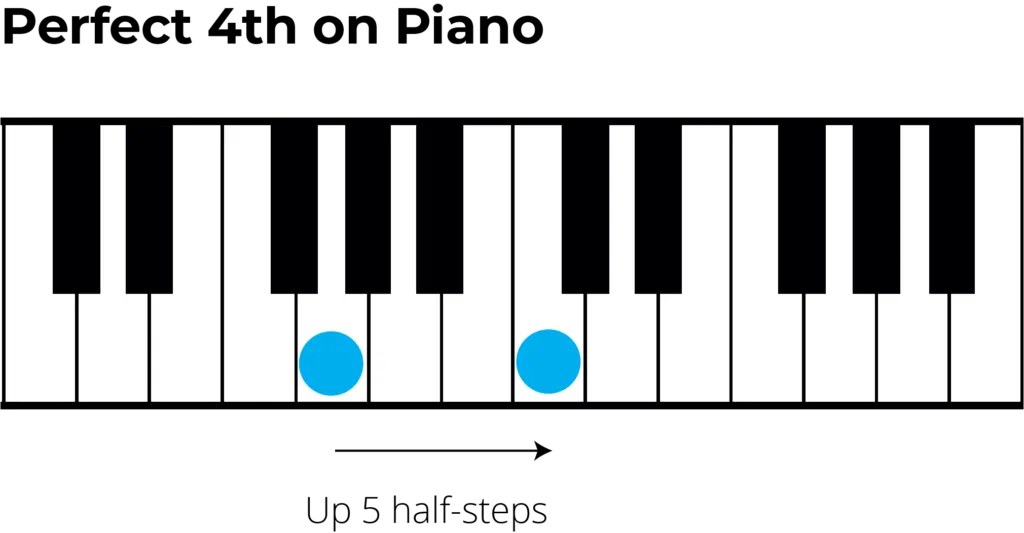
Whereas, the perfect fifth can be seen in Building Triadic Chords from Diatonic Perfect Fifths, from C to G:
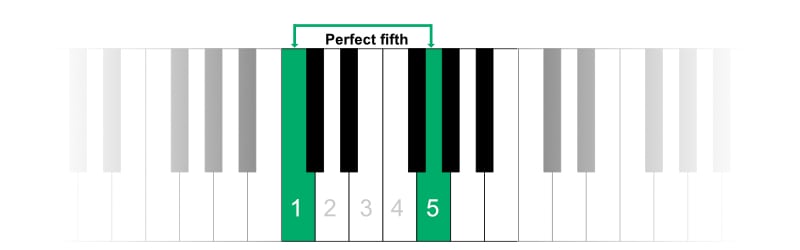
The perfect fifth clearly involves 7, rather than 5, half-steps when their interval is counted within the chromatic scale (i.e., the white and black keys taken together).
Interval Inversion Formula
Since the total of the different numbers of two interval inversions (refer to 20241007141701-Interval_Inversions) must always equal 9, the inversion of any given interval can be calculated thus:
Where is the number for the resolved interval, and is the number for the inversion of the aforementioned interval.
root_position chord_inversion triad_inversion triad_chord_inversion pitch musical_key musical_scale musical_chord interval_inversion procedure procedural_reversal argument_reversal perfect_fifth half-step triad semitone perfect_fourth intervals diatonic chromatic formula algebra mathematics music_theory major_interval minor_interval perfect_interval major_scale C_major_scale
bibliography
- “Interval Inversions.” In Music Theory for Electronic Music Producers: The Producer’s Guide to Harmony, Chord Progressions, and Song Structure in the MIDI Grid., 1st ed., 92. Minneapolis, MN: Slam Academy, 2018.