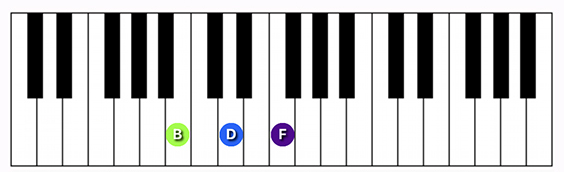
Interval of a 6th
From “The 6th¨ in Music Theory for Electronic Music Producers
The interval of a 6th is the space, move or span of an inclusive count of 6 (mechanical) keys or their corresponding pitches from a musical key of a musical scale up or to the right of a standard Western classical piano keyboard or piano roll editor. In sum, it is an inclusive distance of 6 diatonic (mechanical) keys or their corresponding pitches. The half-step distance in chromatic keys may vary. The below exemplifies a 6th with a major quality starting from C in the key of C major scale (refer to 20240904103821-Musical_Scale_and_Key_Patterns & 20240903174948-Being_“In_Key”), which chromatically has 9 half-steps (refer to 20240831190951-Musical_Alphabet & 20240831200842-Musical_Accidentals).
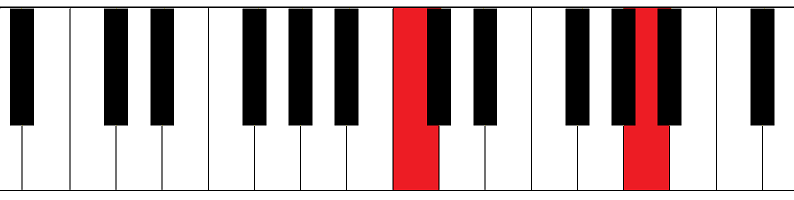
A (diatonic) minor interval of a 6th will likely have a different amount of chromatic half-steps.
Distinguishing Major v. Minor Intervals
For distinguishing major and minor intervals, see Perfect and “Imperfect¨ Inversions.
The interval of a 6th can play the same role as the interval of a 3rd in distinguishing major and minor chords, especially “larger¨ triad chords. Reminder of the way the interval of a 3rd has this role in triad chords:
20240928130915-Two_Thirds_in_Triads
Two Thirds in Triads
Chords
For background on what a chord is, see 20240904095922-Chords & 20240924121346-What_Chords_Are.
From bib. source
[…] in order to make a minor triad we have two thirds: a minor third on the bottom, and a major third on the top. The diminished chord breaks this rule: It is made of two minor thirds.
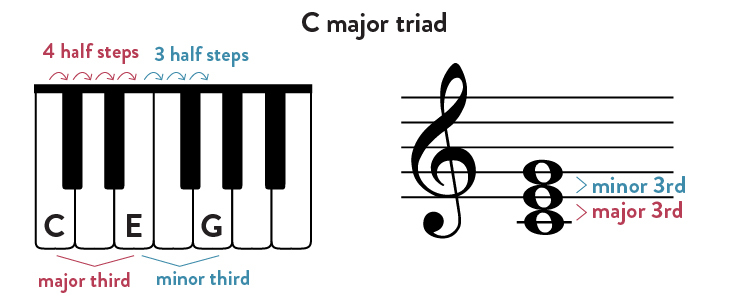
That is, triads are made of “two thirds,¨ with a minor triad having a “minor third¨ on the bottom (i.e., on the right on a standard Western classical piano) and a “major third¨ on the top (i.e., on the left on a standard Western classical piano) (Allen 2018, 79). The converse is the case for a major triad, wherein the minor third is on the top and the major third is on the bottom.
The minor thirds and major thirds of a C major triad chord, built on/from the C Major scale, would look like this:
This can help us understand a little bit more how chords built from a scale sit within the sequence of the musical alphabet with its accidentals:
Chromatic Interval Variability of Diatonic Chords
Further, the D triad from C major scale and the C triad from C major scale both have the same interval relationships in their notes / (mechanical) keys / pitches within their shared scale key, yet their interval relationships actually diverge if one pays attention to the entirety of the musical alphabet together with its accidentals (see 20240831190951-Musical_Alphabet & 20240831200842-Musical_Accidentals).
D Triad v. C Triad Chord Intervals in Key of C Major Scale
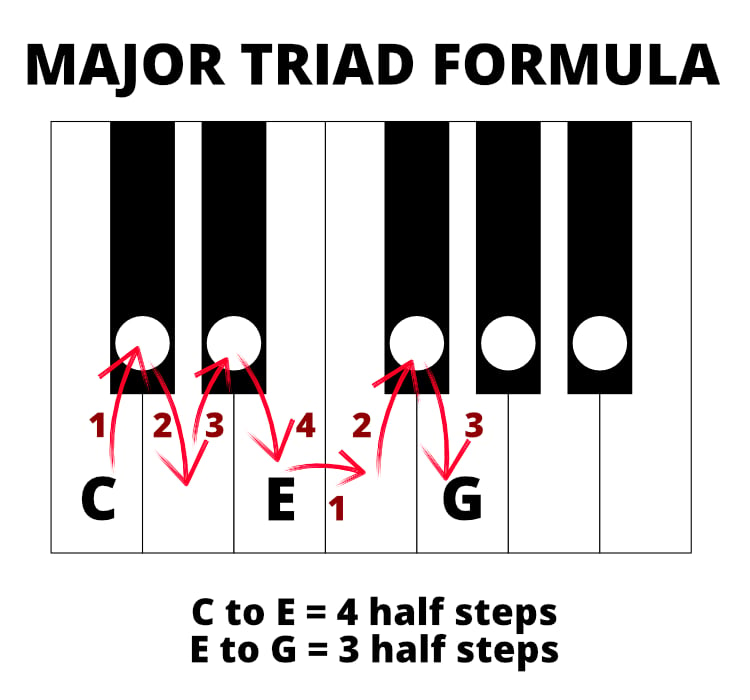
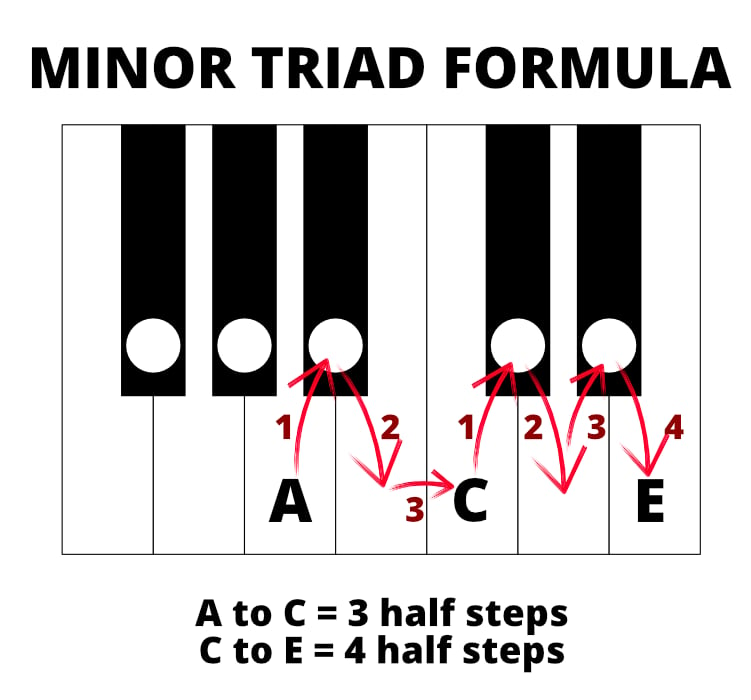
The C triad’s sequence has 4 half-steps from its “first¨ to its “third¨ and 3 half-steps from its “third¨ to its “fifth.¨ Yet the D triad has this reversed in its sequence. This is what makes the D triad from C Major scale a minor chord, and the C triad from C major scale a major chord. Both have the same total of 7 half-steps from start to end.
C triad chord in the key of the C major scale is a major chord:
An A chord triad in the key of the C major scale is a minor chord:
Essentially (Allen 2018, 70 & 72):
From “Major vs Minor¨ in Music Theory for Electronic Music Producers
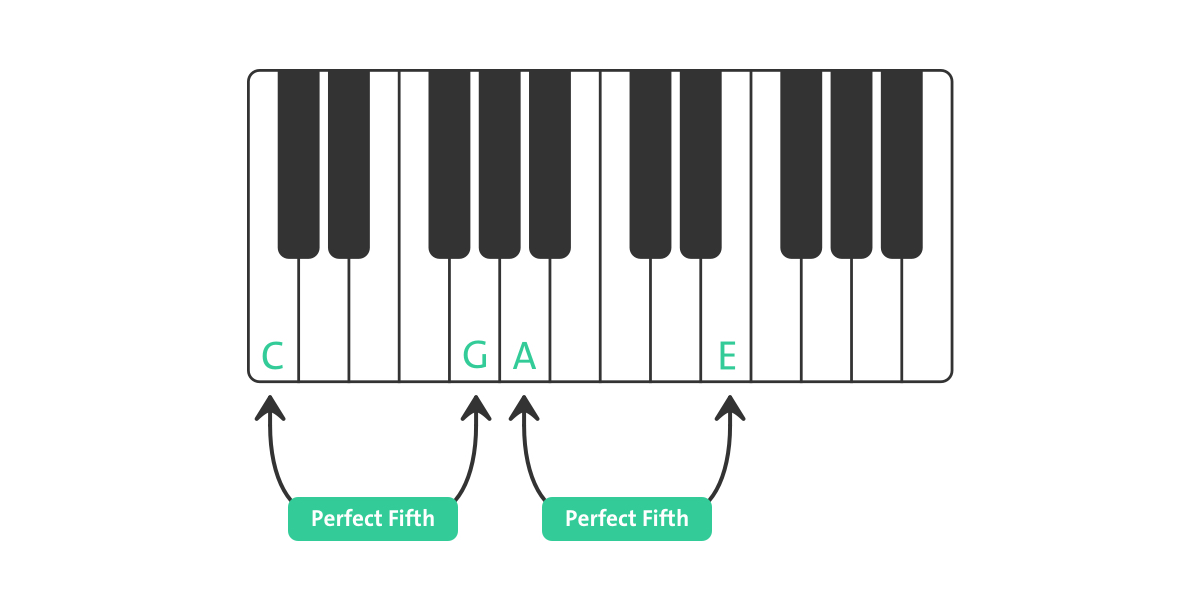
The number of half steps between C and G is seven, and the number of half-steps between D and A is seven. So the distance from the root to the fifth is seven - whether a chord is major or minor - the distance between the root and the fifth stays the same[sic]. The distance between the root and the fifth is an interval that we already know - it’s a perfect 5th. So in order to make a triad, we need a perfect 5th and one note inside of the perfect fifth - the third.
Building Triadic Chords from Diatonic Perfect Fifths
Evidently, another way to think about triads is as perfect fifths, when including all (mechanical) keys / pitches / notes, from the chord root, with a (mechanical) key / pitch / note in-between, the “third¨ (for more on perfect fifths, see 20240901171406-Musical_Intervals) (Allen 2018, 72). Thinking of triads this way makes it easier to practice switching between major and minor triads in the key of a given scale (Ibid):
From “Major vs Minor¨ in Music Theory for Electronic Music Producers
[…] the only difference is the third. And even more clear now is that the different[sic] between the two thirds is just a half-step. If we have a major triad and we want to turn it into a minor triad, you just have to lower the third one half-step. Similarly, if we want to turn a minor triad into a major triad, you just have to raise the third by one half-step.
Examples of perfect fifths in the key of C Major scale (refer to 20240901171406-Musical_Intervals, 20240903174948-Being_“In_Key” & 20240904103821-Musical_Scale_and_Key_Patterns):
major_scale C_major_scale root_key root_pitch root_note chord_root scale_root scale_degree perfect_fifth musical_alphabet intervals scale_degrees conventionalism music_theory musical_scale minor_triad major_triad musical_key half-step semitone chord_quality musical_chord
bibliography
Link to original
- “The Basic Triad.” In Music Theory for Electronic Music Producers: The Producer’s Guide to Harmony, Chord Progressions, and Song Structure in the MIDI Grid., 1st ed., 70–71. Minneapolis, MN: Slam Academy, 2018.
- “Major vs Minor.” In Music Theory for Electronic Music Producers: The Producer’s Guide to Harmony, Chord Progressions, and Song Structure in the MIDI Grid., 1st ed., 72–73. Minneapolis, MN: Slam Academy, 2018.
Defining Minor and Major Thirds
One way of looking at this then is that a minor third is a 3 half-step distance away from the center of a chord triad, while a major third is a 4 half-step distance away from the center of a chord triad.
A diminished chord within this scheme would be comprised of two minor thirds (Ibid):
If you count the half-steps from each key in the triad chord above, you’ll notice that walking from the third (i.e., the second highlighted note / [mechanical] key) is the same 3 half-step distance (refer to Scale Degrees and Triadic Chord Construction for more on what a third is). 3 half-steps is a ”minor third¨ distance in a triad chord.
Diminished Chord Abbreviation
Perhaps “dim¨ then stands for “diminished,¨ to answer the question at the end of 20240927133630-What_is_a_Diatonic_Chord_Progression.
minor_chord major_chord minor_triad major_triad scale musical_scale major_scale minor_third major_third C_major_scale semitone music music_theory musical_alphabet diminished_chord chord_quality musical_key
bibliography
Link to original
- “Diminished Triads.” In Music Theory for Electronic Music Producers: The Producer’s Guide to Harmony, Chord Progressions, and Song Structure in the MIDI Grid., 1st ed., 79. Minneapolis, MN: Slam Academy, 2018.
major_chord chord_inversion interval_quality major_interval minor_interval major_sixth minor_sixth minor_third major_third half-step semitone major_scale C_major_scale music_theory pitch major_6th_interval minor_6th_interval
bibliography
- “The 6th.” In Music Theory for Electronic Music Producers: The Producer’s Guide to Harmony, Chord Progressions, and Song Structure in the MIDI Grid., 1st ed., 95. Minneapolis, MN: Slam Academy, 2018.