Chords from Scales
Chords
For background on what a chord is, see 20240904095922-Chords & 20240924121346-What_Chords_Are.
Building a Chord
From “The Basic Triad¨ in Music Theory for Electronic Music Producers
Lets build a C Major chord.
We are going to start with the root - keep in mind that the root of the chord can be different than the root of the key, or the scale. We can build a D triad using the C Major scale, because it has a D in it.
So long as we know how to build a scale, in particular the Major scale, we know how to build chords from that scale. For a C Major scale in particular, this explanation contains that example:
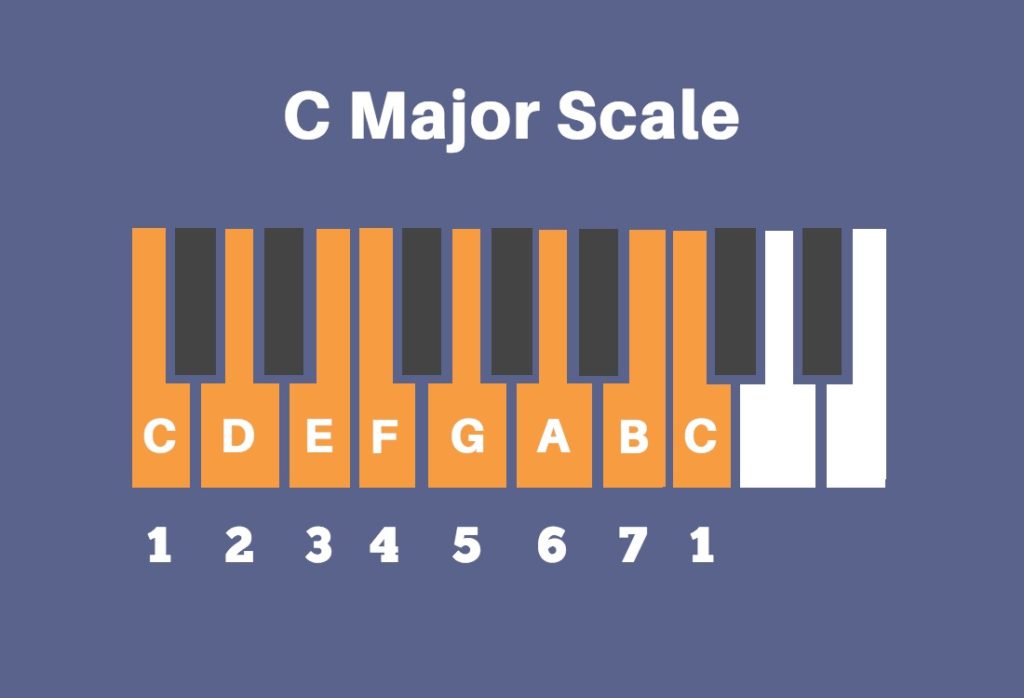
So C Major scale is just the Major scale derived from the root pitch / (mechanical) key C of the musical alphabet (see 20240831190951-Musical_Alphabet).20240904103821-Musical_Scale_and_Key_Patterns
Musical Scale and Key Patterns
From “The Pattern of a Key¨ in Music Theory for Electronic Music Producers
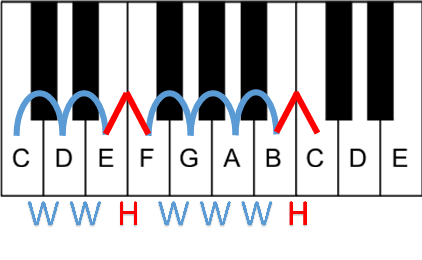
To find the note in any key, we always start with the root. After we have the root, we can apply a pattern made of half-steps and whole steps. This pattern is simply called the major scale. Once we’ve figured out the major scale, we will know all the notes in they[sic] key. The pattern is: W W H W W W H In this pattern, ‘W’ refers to Whole Step and ‘H’ refers to Half-Step.
A musical scale, then, can also be defined more accurately as, not just a sequence of (mechanical) keys or their pitches in order as in 20240903174948-Being_“In_Key”, but a pattern of intervals used for selection of (mechanical) keys and their pitches to comprise a key (qua “in the key of¨). These intervals are the measures half-step and whole step, as explained in 20240831183733-Semitones and 20240901015508-Whole_Tones.
Thus, the root key or root pitch “anchors¨ the scale by acting as the starting key/pitch of the pattern of selection the scale provides.
Reference image for the Major scale with C (natural) as root:
Hence, we get the key of C (Major) using the Major scale on the root C.
flowchart LR A["Root pitch"] -->|Application of scale| C["Produced key"]Note
“W¨ stands for “Whole Tone¨ or “Whole Step,¨ while “H¨ stands for “Semitone¨ or “Half-Step.¨
whole-step whole_step half-step root_key root_pitch musical_scale major_scale music music_theory
bibliography
Link to original
- “The Pattern of a Key.” In Music Theory for Electronic Music Producers: The Producer’s Guide to Harmony, Chord Progressions, and Song Structure in the MIDI Grid., 1st ed., 54. Minneapolis, MN: Slam Academy, 2018.
To build a chord from C major scale, one also needs a root pitch / (mechanical) key (Allen 2018, 70). The root of the chord need not be the same as the root of the scale it was built from so long as the root of the chord resides in the key of C Major (refer to 20240903174948-Being_“In_Key” & 20240904101419-Root_Keys) (Ibid). This would mean that, to build a chord from or “in¨ the key of C Major, we can choose any of the following (mechanical) keys or pitches (the ones in orange):
Scale Degrees and Triadic Chord Construction
Scale Degree Labels
Don’t forget that the scale degrees also have labels: 20240904145213-Supertonic_Scale_Degree, 20240904150953-Mediant_Scale_Degree, 20240904153312-Subdominant_Scale_Degree, 20240904154815-Dominant_Scale_Degree, 20240904161116-Submediant_Scale_Degree, & 20240904162744-Leading_Tone_Scale_Degree.
Conventionally, building a triad itself involves grabbing an interval relationship from the given scale (refer to 20240901171406-Musical_Intervals) (Ibid):
From “The Basic Triad¨ in Music Theory for Electronic Music Producers
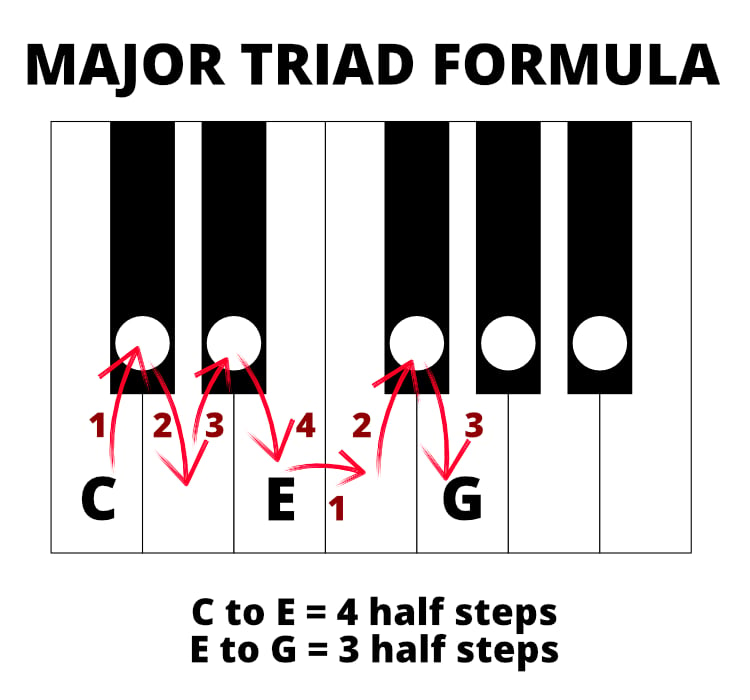
[…] in this case, since we are building a C triad, the root will be C. Next we go up the scale, skipping the next note, D. That takes us to the pitch E. This is our second note that we need. We then skip the fourth note of the scale - F - leading us to the pitch G. This is our third (and final) note of the triad. So the three notes in C triad (in C major) are C - E - G.
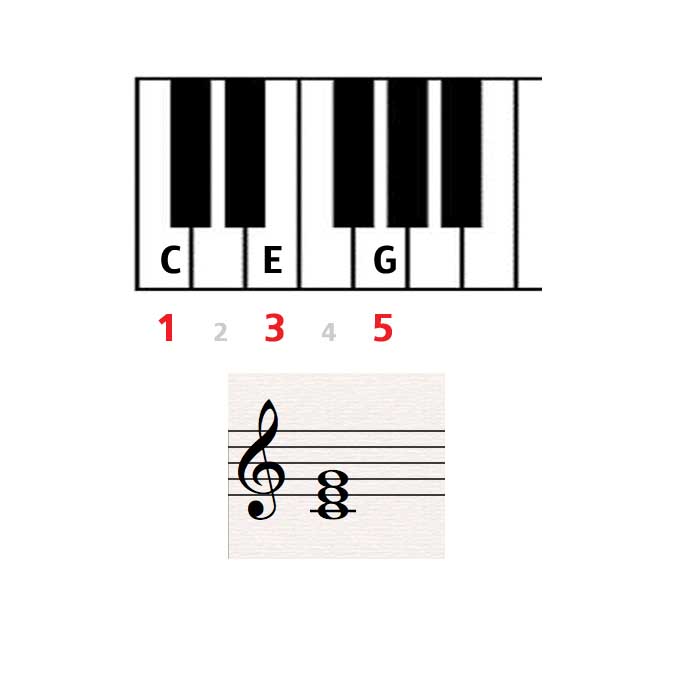
In sum, the composition of a triad can be spoken of in terms of scale degrees (see 20240904131349-Scale_Degrees) (Ibid):
- The first note / pitch / (mechanical) key of a triad chord is the first degree of the given scale
- The second note / pitch / (mechanical) key of a triad chord is the third degree of the given scale
- The third note / pitch / (mechanical) key of a triad chord is the fifth degree of the given scale
This is why (Ibid):
From “The Basic Triad¨ in Music Theory for Electronic Music Producers
When we talk about building chords we often talk about using the, “First, third, and fifth¨.
Caution
Keep in mind that, since the root of a chord can be any pitch / (mechanical) key / note in the key of a given scale, the scale degrees vary. It is the interval relationships within the Major scale key that remain the same for all chords derived from the same scale by this convention. As a holdover, people often still call the (mechanical) keys, pitches or notes in a given chord as if they had the same degrees as those (mechanical) keys, pitches or notes of a chord specifically sharing the same root as the scale it derives from (Ibid).
Example
Chromatic Interval Variability of Diatonic Chords
Further, the D triad from C major scale and the C triad from C major scale both have the same interval relationships in their notes / (mechanical) keys / pitches within their shared scale key, yet their interval relationships actually diverge if one pays attention to the entirety of the musical alphabet together with its accidentals (see 20240831190951-Musical_Alphabet & 20240831200842-Musical_Accidentals).
D Triad v. C Triad Chord Intervals in Key of C Major Scale
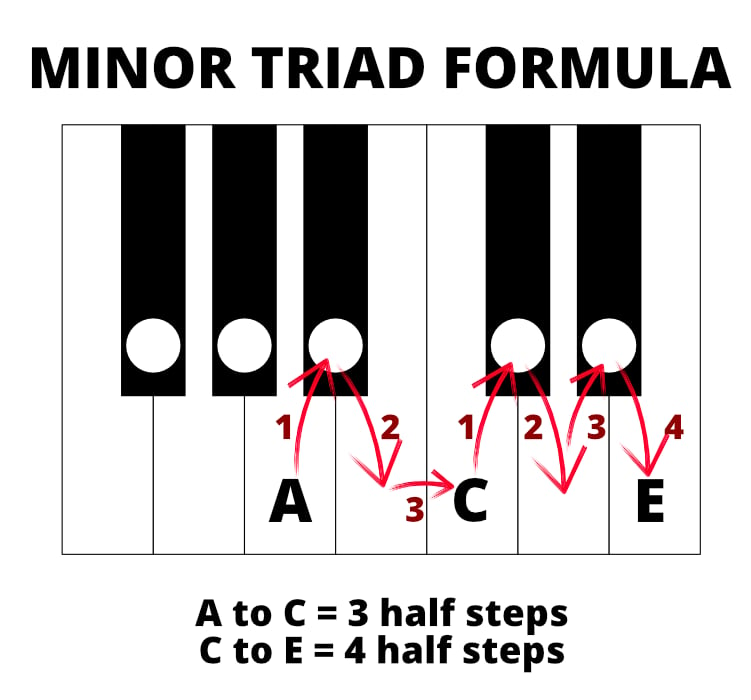
The C triad’s sequence has 4 half-steps from its “first¨ to its “third¨ and 3 half-steps from its “third¨ to its “fifth.¨ Yet the D triad has this reversed in its sequence. This is what makes the D triad from C Major scale a minor chord, and the C triad from C major scale a major chord. Both have the same total of 7 half-steps from start to end.
C triad chord in the key of the C major scale is a major chord:
An A chord triad in the key of the C major scale is a minor chord:
Essentially (Allen 2018, 70 & 72):
From “Major vs Minor¨ in Music Theory for Electronic Music Producers
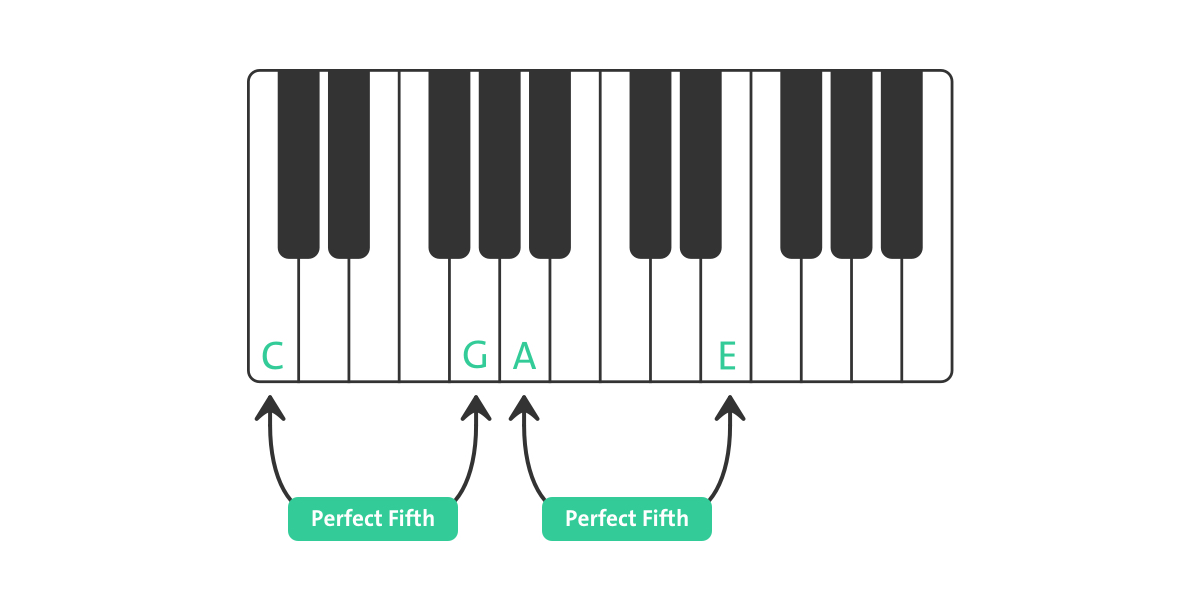
The number of half steps between C and G is seven, and the number of half-steps between D and A is seven. So the distance from the root to the fifth is seven - whether a chord is major or minor - the distance between the root and the fifth stays the same[sic]. The distance between the root and the fifth is an interval that we already know - it’s a perfect 5th. So in order to make a triad, we need a perfect 5th and one note inside of the perfect fifth - the third.
Building Triadic Chords from Diatonic Perfect Fifths
Evidently, another way to think about triads is as perfect fifths, when including all (mechanical) keys / pitches / notes, from the chord root, with a (mechanical) key / pitch / note in-between, the “third¨ (for more on perfect fifths, see 20240901171406-Musical_Intervals) (Allen 2018, 72). Thinking of triads this way makes it easier to practice switching between major and minor triads in the key of a given scale (Ibid):
From “Major vs Minor¨ in Music Theory for Electronic Music Producers
[…] the only difference is the third. And even more clear now is that the different[sic] between the two thirds is just a half-step. If we have a major triad and we want to turn it into a minor triad, you just have to lower the third one half-step. Similarly, if we want to turn a minor triad into a major triad, you just have to raise the third by one half-step.
Examples of perfect fifths in the key of C Major scale (refer to 20240901171406-Musical_Intervals, 20240903174948-Being_“In_Key” & 20240904103821-Musical_Scale_and_Key_Patterns):
major_scale C_major_scale root_key root_pitch root_note chord_root scale_root scale_degree perfect_fifth musical_alphabet intervals scale_degrees conventionalism music_theory musical_scale minor_triad major_triad musical_key half-step semitone chord_quality musical_chord
bibliography
- “The Basic Triad.” In Music Theory for Electronic Music Producers: The Producer’s Guide to Harmony, Chord Progressions, and Song Structure in the MIDI Grid., 1st ed., 70–71. Minneapolis, MN: Slam Academy, 2018.
- “Major vs Minor.” In Music Theory for Electronic Music Producers: The Producer’s Guide to Harmony, Chord Progressions, and Song Structure in the MIDI Grid., 1st ed., 72–73. Minneapolis, MN: Slam Academy, 2018.